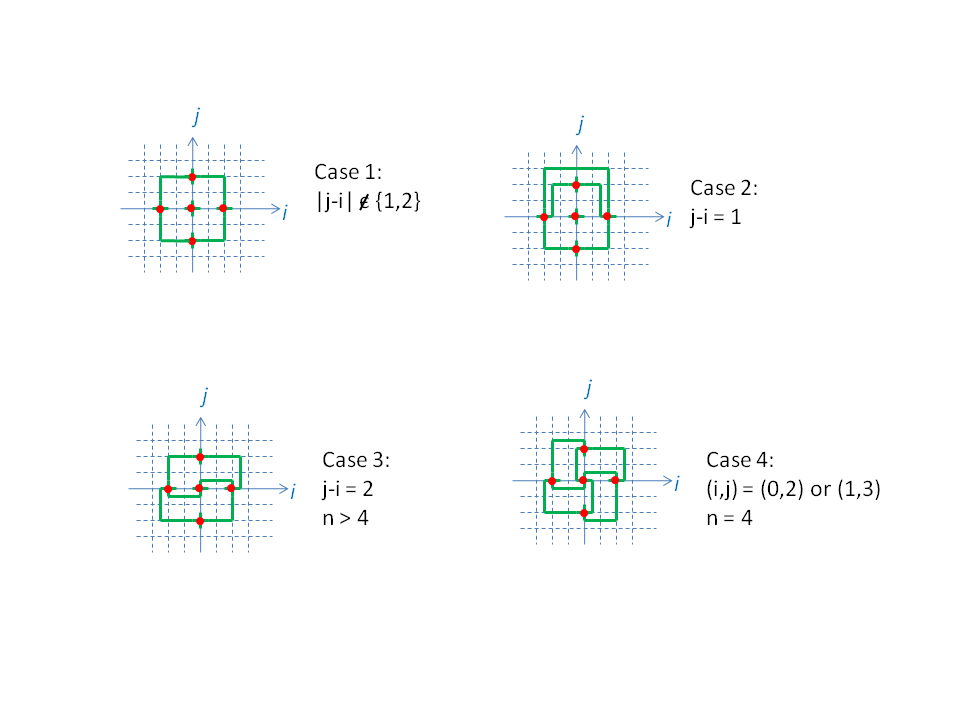
However, because we want the maximal-sized clique embeddable in Rn, we are looking to embed K2n+1. Clearly, no larger cliques are possible, because there are only 2n axis-parallel directions, so no vertex can be connected by more than 2n non-overlapping paths whose initial segments are axis-parallel and joining in a single point.
To do this, let us consider vertices at the origin and at ± each of e1,...,en. To be able to easily ascertain that the construction is valid, all edges will be planar, as in our first construction. Specifically, edges running from ±ei to ±ej will be mapped entirely onto the plane running through ei, ej and the origin. Edges running between ei and -ei will also be on an ei-ej-0 plane, where j will be decided by use of a 1-1 function from i. For example, we can choose j=i+1 (mod n). Similarly, edges running between ±ei and 0 will be mapped entirely onto an ei-ej-0 plane, where j will be decided by use of a 1-1 function from i. In this case, we can choose, for example, j=i+2 (mod n).
If we consider n≥5, cases 1, 2 and 3 in the image below cover every choice of an ei-ej-0 plane. They show cross-sections of a general embedding of K2n+1 in Rn.
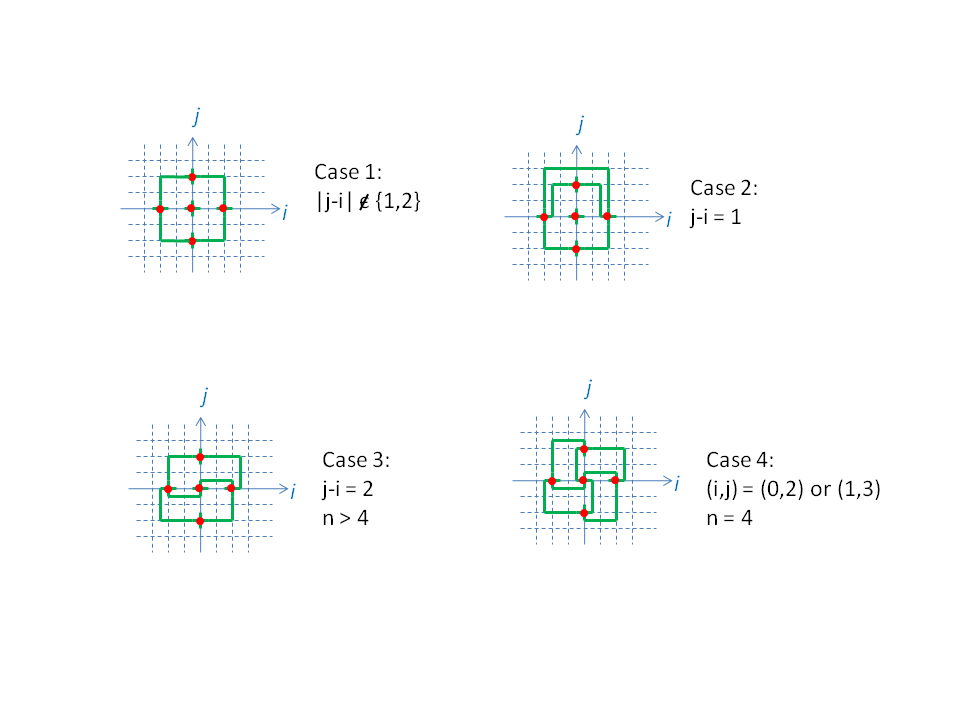
In particular, they present a solution to the R5 problem.
Embedding K9 in R4 is a little more tricky, because some of our plane choices begin to overlap. For example, when i=1 we choose j=3 for the e1-to-0 edge, but when i=3 we choose j=1. This leads both edges to be on the same plane: the one passing through e1, e3 and the origin.
Case 4 in the image above shows how to resolve the resulting difficulties, and presents a solution to R4.
Things become even trickier in R3, where no set of plane-embedded edges seems to provide a valid solution. To solve this case, we are forced to off-center the central vertex. For reasons of symmetry, we will place it at (-0.5,-0.5,-0.5). All edges other than those connecting with this central vertex will still be planar, as before.
The image below shows two solutions for this case. In each image, the dashed lines represent path segments that are not on any ei-ej-0 plane.
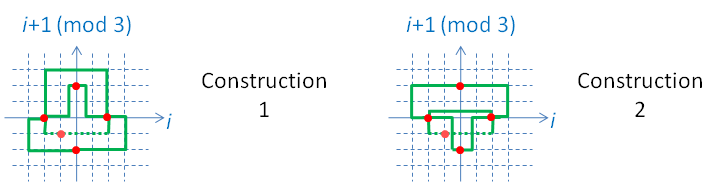
There are three axis-parallel plane directions in R3. Choosing either of the two constructions presented for each of these yields a solution for embedding K7 in R3. It is possible to mix-and-match. Up to symmetries, these are 4 different solutions, depending on how many times one picks the first construction and how many times one picks the second.
The notion that K7 is embeddable in R3 at all is fairly new. It was first shown to be possible only as late as 2000, in David Wood's doctoral thesis. (Up until then this embedding was conjectured not to exist, even though, today, even a simple branch-and-bound program can discover a great many such embeddings in a fairly short run.) Wood describes, in his thesis, a K7 equivalent to choosing "Construction 1" in all three planes. The thesis continues to prove the possibility of embedding K2n+1 in Rn for any n≥3, but does so for higher dimensions using constructions somewhat different than what is presented here.
David Wood's complete thesis can be found here. Also on the same page is a picture of David Wood (right) and Graham Farr (left) along with two wood-and-metal models of 3-D 2-bend point graph embeddings. The left one is K6 and the right one is K7.
Lastly, we reach R2. As we have seen, as one lowers n, the difficulty of finding an embedding of K2n+1 in Rn continuously increases. In n=2 this is actually impossible. The reason for this is that K5 is not a planar graph. However, K4 is embeddable trivially.
For completion, the following links provide text files that solve all four problems.
dim2.txt
dim3.txt
dim4.txt
dim5.txt
Last note: in the literature, the common terminology for this sort of embedding is "orthogonal graph drawing".