The riddle will be given in two parts. Answer either only the first or both for credit.
Part 1:
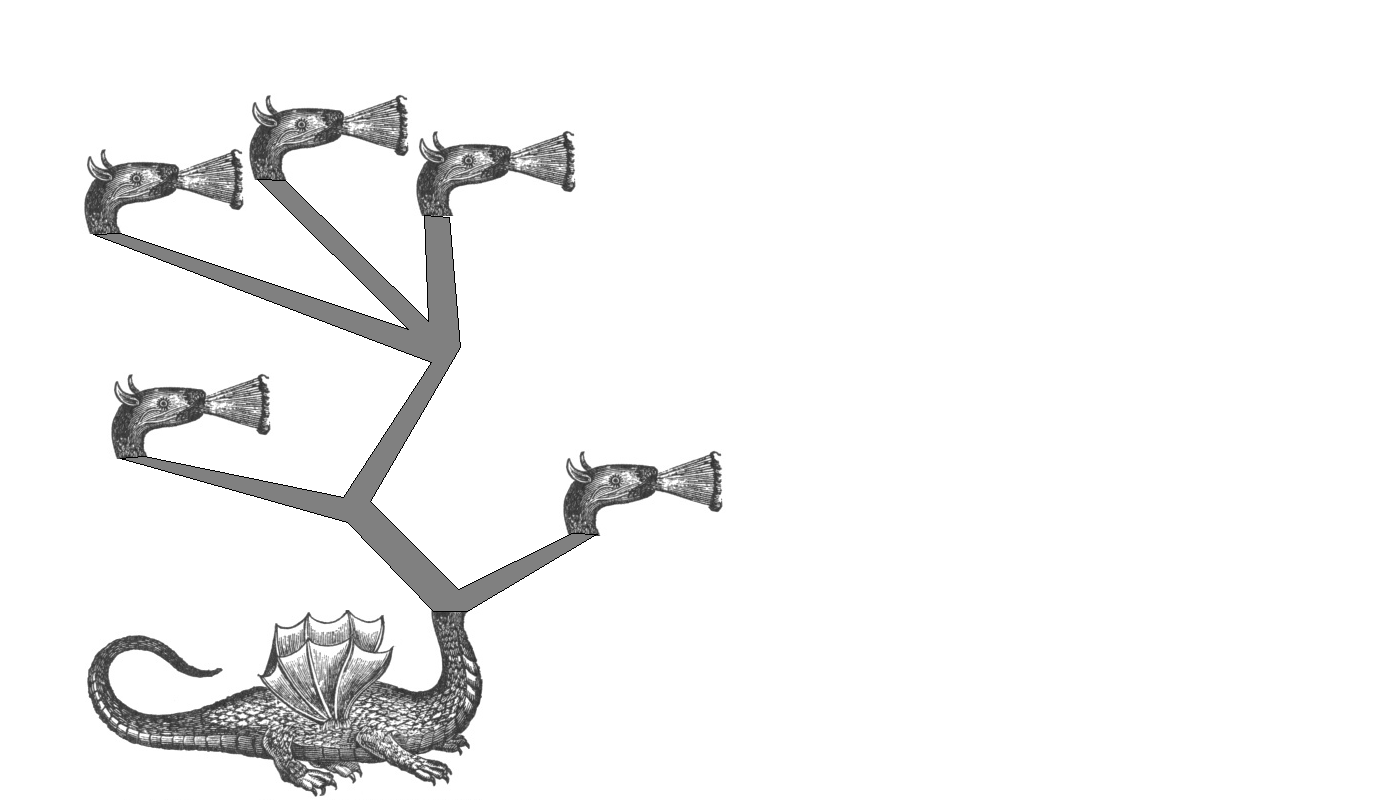
In Greek mythology, Hercules battled the Lernaean Hydra, which was a monster able to regenerate two heads every time one of its heads was chopped off. This has led poets to describe it as a beast with more heads than the pot-makers can draw. What chance could Hercules possibly have against such a monstrosity? Today we find out.Figure 1 shows an example of what battling the hydra may look like.
|
|
| (a) | (b) |
|
|
| (c) | (d) |
Figure 1(a) shows a hydra. For our purposes, a hydra is a tree: the base of the tree is the hydra's body. Its necks are the various branches of the tree, sprouting from joining points that are the nodes of the tree and ultimately terminating in hydra heads which are the leaves of the tree.
When fighting the hydra, Hercules chops off its heads one at a time. Figure 1(b) shows Hercules's sword, depicted here in heroic blue, as it lands on a head which it means to sever.
Upon being hit by the sword, the decapitated hydra loses not only its head but also the adjoining neck. This is depicted in blood red in Figure 1(c). Unfortunately, this is not the end of the story. Unless the neck in question was one that connects directly to the hydra's body (in which case the hydra does not grow back any heads), it is now the hydra's turn to grow heads to replace the lost one. The way this is done is as follows.
First, consider the neck segment going down (towards the body) from the point where the severed piece of the neck fell off. Take this, and everything remaining on it (even if this is an entire, complex tree structure of heads), and duplicate it twice. Figure 1(d) shows this in monster green: two sets of necks grew back to replace the missing head, each sporting two heads on it. All together, because of Hercules's choice with the sword, the hydra gained three heads in this round.
Hercules and the Hydra go on sparring like this for as long as it takes. In each round, Hercules chooses a head, chops it off, waits for the hydra to regenerate and continues. The question is: does this match go on forever (a loss for Hercules) or does Hercules ultimately win by chopping off the last of the Hydra's heads?
More formally:
- For which initial hydra shapes (tree shapes) does Hercules have a strategy to win against the hydra? And if he does, what strategy is it?
- If the hydra, in self-defense, can shield itself, so that only one of its heads is exposed at any given time, that is to say, if it is not Hercules who chooses which head to sever, but the hydra, for which initial hydra shapes does the hydra have a strategy to continue this fight forever?
Part 2:
Part 2 is the same as part 1, with the only difference being the number of heads the hydra regenerates. In the original description, the hydra regenerated two heads (two copies of necks plus everything attached to them) for every lost one. What happens if the hydra regenerates 1 head in the first round, 2 in the second, 3 in the third, and so on, regenerating k heads on the k'th round?This month, as indicated, the riddle is a very old one, classic and well-known. If you want to enjoy it, absolutely no Internet searching, please. The first link you hit will be the solution.
brand.scso.com.
Names of solvers will be posted on this page. Notify if you don't want
your name to be mentioned.