To see this, consider first the following. Let S be a set (finite or infinite) of tuples (x1,...,xn), such that for any a and b, the probability density of (x1,...,xn) is the same for all elements in S. In this case, we may assume that the value of f across all elements of S is the same. If it isn't, we can replace all values of f within S to their expectation given S. This operation does not change the expectation of f (so retains unbiased-ness) and does not increase variance.
An example of such an S is the set of all order permutations over any n values. The probability density is the same regardless of the order of the values (because all values are independent), so we can assume that f is invariant to the order. f can equally be described as getting as input first the minimum valued X, then the second minimum, etc..
More concretely, we will consider f as receiving first the maximum, then the minimum, and then all n-2 other X values, in their original order. Consider how such values can be allotted in this order, without changing the probability density of any outcome. In the new order, the elements are neither uniform nor independent. The first element, max, has the distribution of the maximum of n elements that are uniformly distributed in [a,b]. The second element, given the first, has the distribution of the minimum of n-1 elements that are uniformly distributed in [a,max]. All of the rest of the elements (given the first two) are independent of each other and uniformly distributed in [min,max].
Crucially, because of the uniform distribution of the n-2 latter elements, they can be replaced by any other values within the same range without this affecting probability densities. As such, by our first observation, the function f should only take min and max as its arguments.
It is not difficult to see that f(min,max)=(max+min)/2 is an unbiased estimator. To prove that it is the minimum variance one, suppose on the contrary that there is a g(min,max) that has the same expectation as f but lower variance.
To show that this cannot be, consider the probability density of seeing the pair (min,max) given a and b. To make the calculation simpler, let us initially assume a=0 and b=1.
In this case, the PDF (probability density function) of a uniform random variable is pdf(x)=1 in the range (and 0 outside of the range). Its CDF (cumulative distribution function) is, in the same range, cdf(x)=x, the integral of the PDF. This gives the probability that a uniform random variable X will satisfy X≤x. The probability that n independent variables will satisfy the same is the product of all n CDFs, so xn. That's the probability that the maximum is in the range max≤x. The PDF is the derivative: pdf(max=x)=nxn-1. When scaling this to general a and b, we get:
Every other variable, given the maximum, is independent and uniform in the range [a,max], so the same calculation can be used to calculate the PDF of the minimum of all n-1 of them:
The probability density of getting the pair (min,max) is the product of these two PDFs:
Notably, for a fixed a, b and n, this is proportional to (max-min)n-2.
When we say that a particular estimator, f, is unbiased, we mean that its expectation equals the target value (which, in our case, is (a+b)/2). This expectation is the integral of pdf(min,max)f(min,max) over the area described by the triangle min≥a, max≤b, min≤max. We can, furthermore, take the difference of two such integrals for two unbiased estimators, f and g, and get that the integral of
over this same triangle equals zero. Interestingly, this function does not depend on either a or b. (Only the integration bounds do.) This being the case, let H(a,b) be the integration result (always zero) and consider the calculation that is required to compute
for some small δ>0.
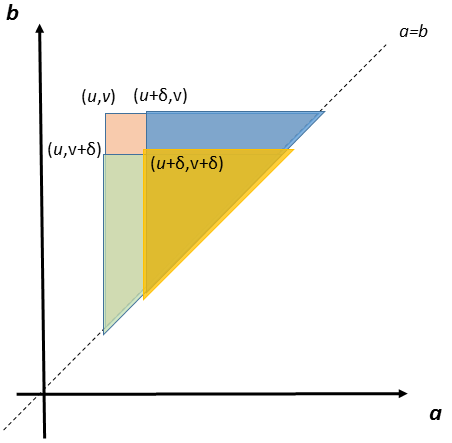
Here is a graphical depiction of what the resulting integration bounds look like.

Ultimately, everything cancels out except for the integral part on a∈[u,u+δ], b∈[v,v+δ], and, as shown previously, the result of this integral must be 0-0-0+0=0.
We have therefore proved that the integral of h is zero in arbitrarily small neighbourhoods around arbitrarily chosen points.
If we can assume that f and g are both continuous functions, if there is a point in which they differ (say, f(x)<g(x)), there will also be an entire neighbourhood in which the same holds and the integral of their weighted difference will not be zero in that neighbourhood.
Without the assumption of continuity, we can say that their difference has zero-measure support, which, in turn, is enough to show that the two estimators' variances will be equal.
Either way, we see that any unbiased estimator that takes only min and max as inputs must be essentially equal to (min+max)/2 and will certainly not have lower variance, and any unbiased estimator that meaningfully depends on any other input cannot have lower variance, either.
Q.E.D.
Curious readers will be interested to know that the actual variance afforded by this estimator is, for a=0, b=1, equal to 1/(2(n+1)(n+2)), so decreasing quadratically with n, as opposed to, for comparison, the unbiased estimator that is the mean of all n variables, whose variance, 1/12n, decreases only linearly.
However, the mid-range is a highly non-robust estimator: even a single ``wrong'' measurement can throw it off arbitrarily far.