Using your Head is Permitted

Best,
Michael.

This month's riddle is an original of mine.

Two of my favourite computer games are 2048 and Sokoban. We already had one riddle dedicated to the former. This month, allow me to introduce my very own mash-up of these two games. I call it Soko-2048-ban.

The game of Soko-2048-ban is played on an infinite, two dimensional board with integer coordinates. Each point on the board begins either empty or with a box whose value is "1". In total, there are 2ⁿ such boxes, for some positive integer n. In addition, in one of the empty positions there is a "worker".

The player controls the worker, and can make it go one step in one of the directions left, right, up and down at every move. The worker has three distinct types of actions that it can perform as it is stepping:

• The worker can move by going into an empty square.
• It can push by moving towards an occupied square, if the next square up is empty. This causes the box in the occupied square to be pushed into the empty square.
• It can compact by moving towards an occupied square, if the next square up is occupied by a square of the same value. This causes the box in the last square to receive the sum of the values of both original boxes.

To exemplify this, consider the following figure.

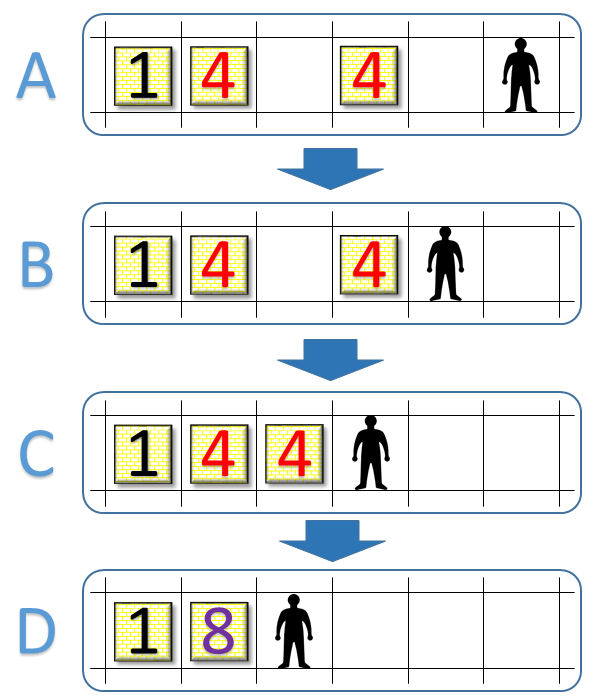
Figure A, at the top, shows a small portion of the infinite board at some intermediate state of the game. The worker is in the right-most position depicted, and to its left are, in order, an empty position, a position with a box whose value is "4", followed by another empty square, another box with a value of "4", and, last, a box whose value is "1".

Suppose, now, that the worker tries to move, repeatedly, to the left.

After one step, it will have arrived to the position depicted in Figure B. The worker has moved into the adjacent empty position and no other change occurred on the board.

After another step to the left, it will have pushed the box of value "4" closest to it into the next position over. This is shown in Figure C.

Lastly, in Figure D, another move to the left compacts the two boxes of value "4" into a single box of value "8".

The worker can at this point no longer move further to the left, because it cannot push the box of value "8" into the box of value "1". Only boxes of identical values can be compacted into each other.

The object of the game is to compact all the boxes, which were originally of value "1", into a single box of value 2ⁿ. This wins the game.

Winning the game requires careful planning. Consider, for example, the figure below, which depicts a possible position in a game that started with 8 boxes.

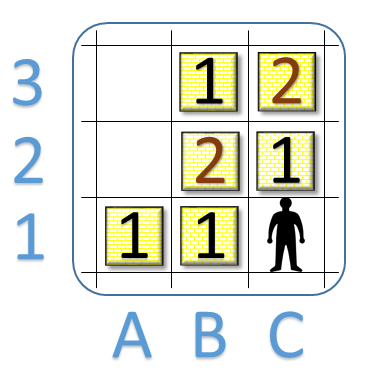
If the worker, at this point in position C1, tries to move left and compact the two boxes of value "1" into each other, it will have by this lost the game, as no sequence of moves following this can lead to a win. (Try finding a move sequence that does solve the game from this position!)

This month's question:
What is the minimal n for which one can construct an initial arrangement of the Soko-2048-ban board that is unwinnable regardless of the player's choice of moves? You are free to choose both the (distinct) initial positions of the "1" boxes and the initial position of the worker (who must be placed on an empty square).

As always, prove your answer.

List of solvers: