Let us assume on the contrary that not all points in S are on the same line. If so, there are members of P for which the distance between the point and the line is nonzero. Because P is a finite set, we can speak of the pair (or pairs) for which this distance is minimal, among all pairs for which the distance is nonzero. Let us pick one of these pairs for which the distance is minimal among the nonzero ones. We will name it <a,l>, where a is the point and l is the line. Let a' be the projection of a on l (meaning that a' is on l and aa' is perpendicular to l). Now, let us divide the points of S on l into two subsets, depending on which side of a' the points are. (a' itself, if it is part of S, will belong to both subsets.)
Per our assumption on the structure of S, there must be at least 3 points of S on l, meaning (using the pigeon-hole theorem) that at least one subset contains 2 points or more. Let us name of these points the one closest to a' by the name b and the one furthest away from a' by the name c. Clearly, c≠a', so the area of the triangle aa'c is positive.
ac belongs to L, so <b,ac> belongs to P. Also, b is clearly not on ac so the distance between b and ac is positive. We claim that the distance between b and ac is less than the distance between a and l, thus contradicting the minimality according to which this pair was chosen. To see this, consider the following:
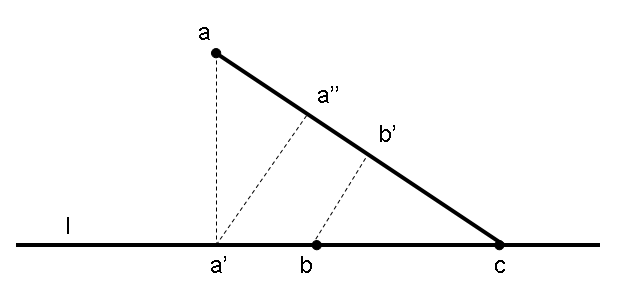
Let b' be the projection of b on ac. bb' is the distance from b to ac and aa' is the distance from a to l, so our claim is that bb'<aa'. Let a'' be the projection of a' on ac. Due to triangle similarity, bb'≤a'a''. We claim a'a''<aa', thus proving the point by transitivity.
Note that aa' ⋅ a'c = a'a'' ⋅ ac equals twice the (positive) area of the triangle aa'c. On the other hand, ac is the hypotenuse of this straight-edged triangle, so it must be longer than a'c which is one of the sides. From the equality of area, we therefore obtain aa'>a'a'': a contradiction.
Q.E.D.
