To see this, note that picking any n vertices will lead to a Kn induced subgraph. There are more ways to pick 3 of 6 than to pick any other number from 6.
Suppose, to the contrary, that such a graph, G, had existed.
Let L(G) be the set of L2 induced subgraphs in G. (L2 is the path of length 2: three vertices connected by 2 edges.) Let S(x), for x in L(G), be the number of distinct ways x can be completed to a C4 by the addition of a vertex. Finally, let Xi be the number of x in L(G) for which S(x)=i.
Using the Xi we can count the number of C4 copies.
The reason we need to divide by four is because each square is counted four times (due to symmetries): each of its four induced copies of L2 can be expanded into a C4.
However, we can also count other subgraphs in the same way. The simplest of these is the count of L2 copies.
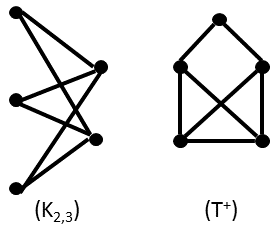
Similarly, for each x in L(G) we can create a graph by picking two of its possible completions into a square, instead of just one. This means picking a shape with 5 vertices: the original 3 plus 2 new ones. The shape of the resulting graph can be one of two, depending on whether the two new vertices are connected by an edge or not.
We call the shape without an extra edge K2,3 and the one with an extra edge T+.

Together, we have the equation
Here, i(i-1)/2 signifies the number of ways to pick pairs from i items, and the multiplication by 3 comes, again, from symmetries.
Consider now the following equation.
If C4 is the most common induced subgraph, the left hand side of this equation should be positive, because it is the number of C4 copies minus a weighted average of the number of copies of three other graphs. (If the result is zero or less, at least one of the other graphs has as many copies as C4 or more.)
On the other hand, the right hand side of the equation must be non-positive, because the amount in parentheses, (-1/16 i2 + 5/16 i -1/2) = -1/16 (i-5/2)2-7/64, is always negative. (It reaches its maximal value, -7/64, at i=2.5.)
We therefore reach an impossibility.
Q.E.D.
Two remarks: