Using your Head is Permitted

This month's question comes from Srinibas Swain. (Thanks, Srinibas!) It has two parts. Answer both for credit.

Part 1:

Part 2:

Some explanations regarding the terminology:

1. A "graph" is a set of vertices and a set of edges connecting pairs of vertices.
2. An "induced subgraph" of a graph G is the graph created by picking a subset of the vertices and all edges connecting them. The order in which vertices are picked is immaterial.
3. The number of appearances of a graph, G, as an induced subgraph of another graph, H, is the number of distinct induced subgraphs of H that are isomorphic to G (i.e., have the same shape). For G to be the most common induced subgraph of H requires for the number of appearances of G as an induced subgraph of H to be strictly larger than the number of appearances of any other connected G' as an induced subgraph of H.
4. C₃ is the cycle of length three, i.e. the triangle. (See image (a) below.) C₄ is the cycle of length four, i.e. the square. (See image (b) below.)

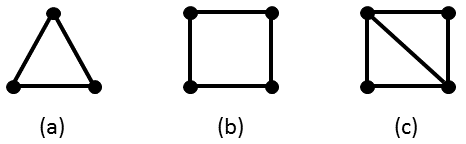
In the graph of image (c), as an example, C₃ appears twice as an induced subgraph, but C₄ does not appear at all. (It appears as a subgraph, but not as an induced subgraph, because an induced subgraph includes all edges connecting the subset of vertices chosen.) The most common induced subgraph of the graph of image (c) is the single edge. It appears 5 times.

List of solvers: